Recursion

What is Recursion? A function calling itself right?

But it's not that simple.

I had watched Utkarsh Gupta's video on Recursion a few weeks ago. He builds upon the concept from the ground up and he emphasizes to Trust the Function.

Recursion = Base case + trust the function

Let's understand with a simple problem.

Problem 01

• Print the first N natural numbers.
• Input : N=7
• Output : 1 2 3 4 5 6 7

This problem can be solved using a simple for loop, but for the sake of understanding let's try to solve the problem using recursion.

Think : Let's print the Nth number and trust the function to print remaining N-1 numbers.

#include<iostream>
using namespace std;
 
void printNumbers(int n){
  if(n==0){
    return;
  }
  printNumbers(n-1); // TRUST THE FUNCTION
  cout << n << " ";
}
 
int main(){
  printNumbers(5); // 1 2 3 4 5
}

But altering only two lines reverses the ouput of the program. Why?

#include<iostream>
using namespace std;
 
void printNumbers(int n){
  if(n==0){
    return;
  }
  cout << n << " ";
  printNumbers(n-1); // TRUST THE FUNCTION
}
 
int main(){
  printNumbers(5); // 5 4 3 2 1
}

Can you draw the recursive tree of the algorithms and conclude the following:

• Time Complexity : O(N)
• Space Complexit : O(1)

Problem 02

• Find the Nth Fibonacci number.
• Input : 6
• Ouput : 21
• Explaination : 1,1,2,3,5,8

The definition of Fibonacci Sequence gives away the recursive expression. As the Nth number is sum of (N-1)th and (N-2)th number, the recursion expression is:

Fib(N) = Fib(N-1) + Fib(N-2), N>2 where Fib(1)=1, Fib(1)=1

#include<iostream>
using namespace std;
 
int fib(int n){
  if(n==1) return 1;
  if(n==2) return 1;
 
  return fib(n-1) + fib(n-2); // TRUST THE FUNCTION
}
 
int main(){
  cout << fib(8) << "\n"; // 8
}

Refer to the recursive tree below.

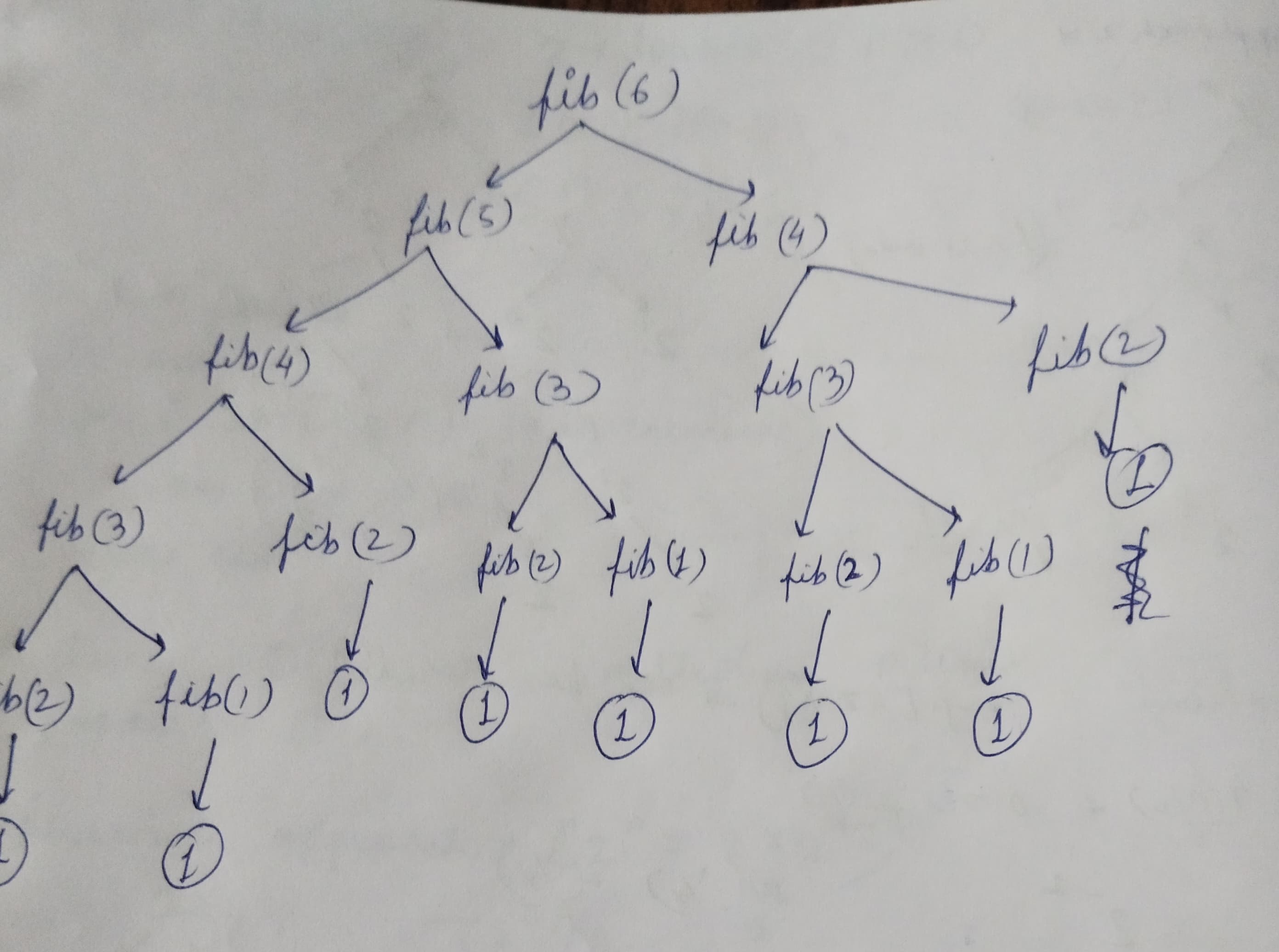
• Time complexity : O(NlogN) why?
• Space complexity : O(1)

You can observe that the algorithms computes the same value multiple times. For example the right half of the tree, fib(4) is previously computed. We can use Memoization to optimize the algorithm.

#include<iostream>
#include<map>
using namespace std;
 
map<int,int> memo;
int fib(int n){
  if(n==1) return 1;
  if(n==2) return 1;
 
  if(memo.find(n) != mp.end()){
    return memo[n];
  }
  int memo[n] = fib(n-1) + fib(n-2);
 
  return memo[n]; // TRUST THE FUNCTION
}
 
int main(){
  cout << fib(8) << "\n"; // 8
}

Now that we understand the basics of recursion, let's solve a problem.

Problem 03 : Pow(x,n)

Implement pow(x, n), which calculates x raised to the power n (i.e., x^n). For full problem description refer directly to Leetcode.

Example 1:

• Input: x = 2.10000, n = 3
• Output: 9.26100

Example 2:

• Input: x = 2.00000, n = -2
• Output: 0.25000 Explanation: 2-2 = 1/22 = 1/4 = 0.25

Approach 01 : Brute Force

The first approach that occurred to me was to multiply x to itself n times. That's what exponentiation is, right? i.e 2^4 = 2*2*2*2

#include<iostream>
using namespace std;
 
double naivePow(double x, int n){
  double ans = 1;
  if(n==0){
    return 1;
  }else if(n>0){
    for(int i=1;i<=n;i++){
      ans*=x;
    }
  }else{
    for(int i=n;i<0;i++){
      ans/=x;
    }
  }
  return ans;
}

We also need to keep in mind the case when n<0, so instead of multipying n times we need to divide.

• Time : O(N)
• Space : O(1)
• Verdict : Time Limit Exceeded

Approach 02 : Recursive

Try to think it this way:

• 2^4 = 2 * 2^3
• 2^3 = 2 * 2^2
• 2^2 = 2 * 2^1
• 2^1 = 2

Think : We trust the function to calculate the x^(n-1) and then multiply with x

double PowRecurse(double x, int n) {
  if(n==0){
    return 1;
  }else if(n>0){
    return x * PowRecurse(x,n-1);
  }else {
    return (1/x) * PowRecurse(x,n+1);
  }
}

observe that we handle the case for positive and negative powers separately.

• Recursive Expression : T(N) = 2*T(N/2) + c , why?
• Time : O(N)
• Space : O(1)
• Verdict : Time Limit Exceeded

Approach 03 : Recursive by splitting in half

Think : We can write 2^10 as

• 2^10 = 2^5 * 2^5;
• 2^5 = 2 * 2^4;
• 2^4 = 2^2 * 2^2 and so on.

Based on whether n is even or odd, we can split the tree and recurse.

double myPowRecurseOptimal(double x, int n) {
  if(n==0){
    return 1;
  }else if(n>0){
    return n%2==0 ? myPowRecurse(x,n/2) * myPowRecurse(x,n/2) : x * myPowRecurse(x,n-1);
  }else {
    return n%2==0 ? myPowRecurse(x,n/2) * myPowRecurse(x,n/2) : 1/x * myPowRecurse(x,n+1);
  }
}

• Time : I think it's still O(N)?
• Space : O(1)
• Verdict : Time Limit Exceeded

Approach 04 : Binary exponentiation

After getting TLE thrice, I watched a video on YouTube.

Given the constraints on n, (-2^31 <= n <= 2&31-1), we need an algorithm that runs in O(logN) time.

Any decimal number N, has atmost log(N)+1 digits in its binary form.

For example , n=5 can be written in binary as 101. To calculate x=3, n=5 we can simply multiply the powers 3^1 and 3^4 when the binary form has a 1.

We keep calculating the sqaures of x and multiply in ans if in binary form of n the last digit is 1.

double myPow(double x, int n) {
  if(n==0) return 1.0;
  if(n==1) return x;
  if(x==0) return 0.0;
  if(x==-1 && n%2==0) return 1.0;
  if(x==-1 && n%2!=0) return -1.0;
 
  long bin = n;
  if(n<0){
      x = 1/x;
      bin = -bin;
  }
 
  double ans = 1;
 
  while(bin > 0){
      if(bin%2==1){
          ans*=x;
      }
      x*=x;
      bin/=2;
  }
 
  return ans;
  }

• Time : O(logN)
• Space : O(1)
• Verdict : Accepted

Fin

Today I refreshed the basics of recursion, understanding how to think recursively. The next step is to understand how to find recursive expression for any algorithm and find it's time and space complexity. I am going to read more on recursion and analysis of algorithms from the book "Introduction to Algorithms". If there are any mistakes please let me know. Thanks!